01
no 05
Algebrisko izteiksmju 1. darblapa
Drukājiet PDF darblapu iepriekš, atbildes ir otrajā lappusē.
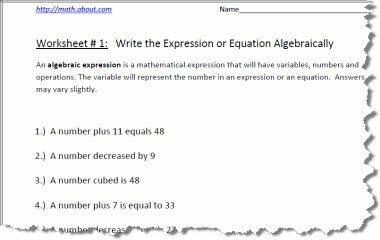
Algebriska izteiksme ir matemātiska izteiksme, kurai būs mainīgie, skaitļi un operācijas. Mainīgais apzīmē skaitli izteiksmē vai vienādojumā. Atbildes var nedaudz atšķirties. Spēja rakstīt izteiksmes vai vienādojumus algebriski ir pirmsalgebras jēdziens, kas nepieciešams pirms uzņemšanas algebra.
Pirms darblapu veidošanas ir nepieciešamas šādas iepriekšējas zināšanas:
02
no 05
Algebriskās izteiksmes 2. darblapa
Drukājiet PDF darblapu iepriekš, atbildes ir otrajā lappusē.
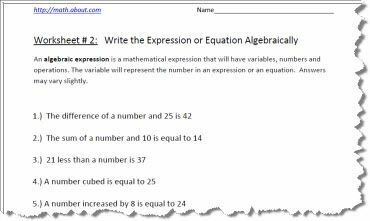
Algebrisko izteiksmju vai vienādojumu izrakstīšana un procesa iepazīšana ir galvenā prasme, kas nepieciešama pirms algebrisko vienādojumu vienkāršošanas. Ir svarīgi izmantot. atsaucoties uz reizināšanu, jo jūs nevēlaties sajaukt reizināšanu ar mainīgo x. Lai gan atbildes ir sniegtas PDF darblapas otrajā lappusē, tās var nedaudz atšķirties atkarībā no burta, kuru izmanto, lai attēlotu nezināmo. Kad redzat paziņojumus, piemēram:
Cipars pieci ir simts divdesmit, tā vietā, lai rakstītu n x 5 = 120, jūs rakstītu 5n = 120, 5n nozīmē reizināt skaitli ar 5.
03
no 05
Algebriskās izteiksmes 3. darblapa
Drukājiet PDF darblapu iepriekš, atbildes ir otrajā lappusē.
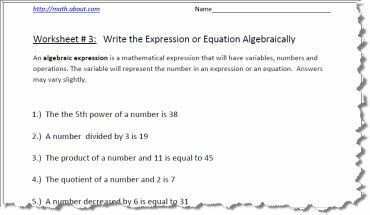
Algebriski izteicieni ir nepieciešami mācību programmā jau 7. klasē, tomēr pamati uzdevumu izpildei rodas 6. klasē. Domāšana algebriski notiek, lietojot nezināmās valodas valodu un attēlojot nezināmo ar burtu. Iesniedzot jautājumu, piemēram: Starpība starp skaitli un 25 ir 42. Atšķirībai vajadzētu nozīmēt, ka tiek ietverta atņemšana, un, zinot to, apgalvojums izskatās šādi: n - 24 = 42. Ar praksi tas kļūst par otro dabu!
Man bija skolotājs, kurš man reiz teica, atcerieties noteikumu 7 un apmeklējiet vēlreiz. Viņš uzskatīja, ka, ja jūs izpildīsit septiņas darba lapas un atkārtoti apmeklēsit koncepciju, jūs varētu apgalvot, ka jūs atradīsities izpratnes vietā. Līdz šim šķiet, ka tas ir darbojies.